VIDEO PEMBELAJARAN VIII | POLA BILANGAN | 1. Menentukan persamaan dari suatu barisan bilangan

Hi Assalamualaikum Moorid Moorid 💛

بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم

Selamat menyimak video tentang Menentukan persamaan dari suatu barisan bilangan.

Read More

VIDEO PEMBELAJARAN VII | BILANGAN BULAT | 1. Konsep dan Membandingkan Bilangan Bulat

Hi Assalamualaikum Moorid Moorid 💛

بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم

Selamat menyimak video tentang konsep dan membandingkan bilangan bulat.

Read More

POLA BILANGAN | 2. Menentukan Persamaan dari Suatu Konfigurasi Objek

Hi Assalamualaikum Moorid Moorid 💛

Pola Unik yang dihasilkan oleh pola bilangan fibonacci

Senang sekali mengetahui kalian tetap bersemangat melakukan proses pembelajaran. Sebelum memulai aktivitas belajar, mari awali dengan berdoa. 

Selalu bersyukur kepada Allah Yang Maha Esa atas segala nikmat yang diberikan, semoga kalian diberi kemudahan dan keberkahan dalam belajar. Jagalah kesehatan mengingat saat ini coronavirus sedang mewabah. Lakukanlah perlindungan diri dengan cara rajin mencuci tangan memakai sabun, menjaga jarak dan mengenakan masker kesehatan. Selamat belajar!

Mari kita lanjutkan dengan mengisi kehadiran melalui link bawah ini (klik sesuai kelas) jika sudah mengisi kehadiran di GOOGLE CLASSROOM maka tidak perlu mengisi lagi:

KELAS 8A            KELAS 8B          KELAS 8C         KELAS 8D        

Masih ingat dengan pola bilangan yang sudah kita pelajari pada sesi lalu? Yuk kita ingat kembali definisinya.

Pola bilangan matematika adalah susunan dari beberapa angka yang dapat membentuk pola tertentu. Pola bilangan juga bisa diartikan sebagai suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola.

Pada kesempatan kali ini kita akan mempelajari tentang jenis-jenis pola bilangan berdasarkan konfigurasinya. Perhatikan dan amati gambar di bawah ini!

1. Pola Bilangan Ganjil

Bilangan 1, 3, 5, 7, …………… dapat membentuk suatu pola bilangan ganjil yang dimulai dari angka 1 dan selanjutnya tinggal menambahkan 2 dalam bilangan sebelumnya.

Secara umum pola bilangan ganjil ini dapat kita gambarkan sebagai berikut:

Rumus untuk mencari pola bilangan ganjil adalah

Un = 2n – 1

2. Pola Bilangan Genap

Bilangan 2, 4, 6, 8, …………… dapat membentuk suatu pola bilangan yang disebut dengan pola bilangan genap. Pola bilangan ini dimulai dari angka 2 dan selanjutnya didapat denagn menambahkan 2 dalam bilangan sebelumnya.

Secara umum pola bilangan genap dapat digambarkan sebagai berikut:

Rumus untuk mencari pola bilangan genap adalah

Un = 2n

3. Pola Bilangan Fibonacci

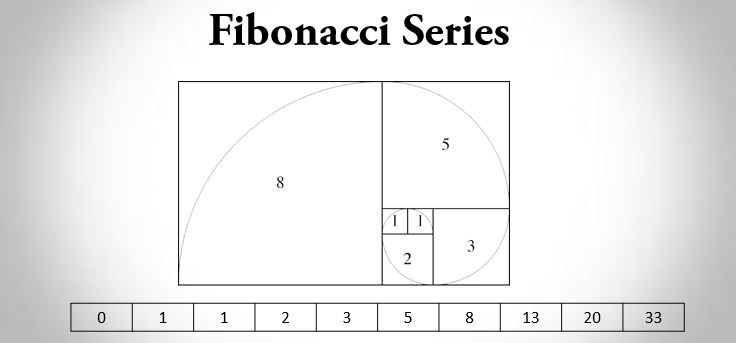
Pola bilangan fibonacci merupakan sebuah bilangan dimana setiap suku bilangannya merupakan jumlah dari 2 suku di depanya. Contoh Pola bilangan fibonacci:

1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 56 , 90, . . .
2 , 2 , 4 , 6 , 10 , 16 , 26 , 42 , 68. . ..
3, 6, 9, 15, 24, 39, 63, …..

0, 1, 1, 2, 3, 5, 8, 13, 20, 33, .... 

trytoprogram.com

  

4. Pola Bilangan Segitiga

Pola bilangan ini terdiri dari angka-angka 1, 3, 6, 10, 15, ……. Bilangan tersebut dihasilkan dari penjumlahan bilangan cacah berurutan yang dimulai dari:

0 + 1 = 1
0 + 1 + 2 = 3
0 + 1 + 2 + 3 = 6
0 + 1 + 2 + 3 + 4 = 10
0 + 1 + 2 + 3 + 4 + 5 = 15
0 + 1 + 2 + 3 + 4 + 5 + 6 = 21 dan seterusnya

Sehingga jika digambarkan akan membentuk pola segitiga seperti ini:

        Contoh Pola Segitiga

        Jadi, pola barisan bilangan segitiga ialah berbentuk n(n + 1)/2

 5. Pola Bilangan Persegi

Pola bilangan ini terdiri dari angka-angka 1, 4, 9, 16, 25, 36, ………… dan bilangan tersebut dapat didapat dari kuadrat bilangan asli

1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36 dan seterusnya

Sehingga jika digambarkan akan tampak membentuk persegi seperti ini:

Contoh Pola Persegi

6. Pola Bilangan Persegi Panjang

Ini mirip dengan persegi, ini bentuk visual dari bilangan yang mirip dengan persegi.

Jika kita perhatikan 6 suku pertama bilangan persegi panjang yakni: 2,6,12,20,30, dan 42

Jadi bentuk pola barisan bilangan persegi panjang pada suku ke-n ialah n(n + 1).

 7. Pola Bilangan Pascal

Pola ini sedikit berbeda dengan bilangan sebelumnya karena pola ini terbentuk dari segitiga pascal yang berbentuk seperti

Bilangan yang warnanya merah disebut sebagai barisan bilangan pascal, Jadi pola bilngan segitiga pascal ialah 2n-1

Alhamdulillah materi sudah selesai. Selanjutnya kita akan menguji pemahaman kita mengenai materi yang baru saja kita pelajari dengan cara mengerjakan Kuis 2 via Googleform di bawah ini. Selamat mengerjakan.

KUIS 2 CEK

Stay Happy, Stay healthy 💛 Ibook Kiki

Read More

POLA BILANGAN | 1. Menentukan Persamaan dari Suatu Barisan Bilangan

Hi Assalamualaikum Moorid Moorid 💛

Susunan bola billiard

Pada kegiatan kali ini kita akan mempelajari tentang "POLA BILANGAN". Namun sebelum kita mulai belajar, mari kita sama-sama berdoa agar pembelajaran hari ini lancar dan lanjutkan dengan mengisi kehadiran melalui link bawah ini (klik sesuai kelas):

KELAS 8A            KELAS 8B          KELAS 8C         KELAS 8D     

Kita awali pembahasan materi pada hari ini dengan menyimak video di bawah ini:

VIDEO POLA BILANGAN 1

Jika kegiatan menyimak video sudah selesai, silahkan baca dengan seksama materi di bawah ini. Buatlah catatan penting di buku kalian.

Pernahkah kalian menyaksikan permainan billiard? Coba kalian perhatikan bola-bola yang digunakan dalam permainan billiard di atas. Sebelum permainan billiard dimulai, bola-bola disusun membentuk susunan segitiga di tengah-tengah meja billiard. Susunan bola-bola tersebut membentuk sebuah pola bilangan yang menarik.

Di barisan paling atas terdapat 1 bola

Di barisan kedua terdapat 2 bola

Di barisan ketiga 3 bola

Di barisan keempat 4 bola

Di barisan kelima 5 bola

Susunan bola billiard, membentuk sebuah pola bilangan asli, 1, 2, 3, 4, 5.

Dapatkah kalian menebak banyaknya bola pada barisan kedelapan?

Mari kita perhatikan bola-bola pada billiard yang berada di sisi sebelah kanan!

Jika angka-angka pada bola billiard kita susun, maka akan membentuk suatu pola

1 , 3,  6, 10, 15, ...

Dapatkah kalian menentukan nomor bola selanjutnya?

Dari 2 cerita di atas, kita menemukan bahwa bilangan-bilangan tersebut memiliki susunan yang teratur.

Kumpulan bilangan-bilangan tersebut disusun dengan pola tertentu, yang di sebut dengan POLA BILANGAN.

Seperti pada cerita pertama, susunan bola billiard membentuk pola bilangan asli yaitu 1, 2, 3, 4, 5 ... dst yang memiliki pola teratur "Bilangan selanjutnya dihasilkan dari penjumlahan 1"

Pada cerita kedua, susunan angka pada bola billiard membentuk pola bilangan yang teratur yaitu 1, 3, 6, 10, 15, ... dst yang memiliki pola teratur "Bilangan selanjutnya dihasilkan dari penjumlahan 2, 3, 4, 5 dan seterusnya"

Pola bilangan ini adalah contoh pola bilangan bertingkat.

Untuk lebih memahami tentang pola bilangan mari kita simak masalah di bawah ini!

Masalah 1: Pita Merah Putih

Seorang murid hendak membeli hiasan pita sepanjang 121 kotak, berwarna merah putih untuk menghias kelas. Bentuk pitanya seperti gambar di bawah ini!

Warna apakah yang terdapat pada kotak 121?

Penyelesaian 1:

Pola bilangan berwarna merah adalah pola bilangan 0 dan genap : 0, 2, 4, 6, 8, 10, ...

Pola bilangan berwarna putih adalah pola bilangan ganjil : 1, 3, 5, 7, 9, ...

Angka 121 merupakan bilangan ganjil, sehingga warna yang ada di kotak 121 adalah putih.

Masalah 2: Pita Merah Putih Biru

Kali ini seorang murid kembali lagi ke toko pita untuk membeli hiasan pita berwarna merah putih biru dengan ukuran 437 kotak. Bentuk pitanya seperti gambar di bawah ini!

Kali ini warna apakah yang terdapat pada kotak ke 437?

Penyelesaian 2:

• Pita berwarna merah memiliki pola bilangan selalu bertambah 3 atau kelipatan 3. Sehingga angka-angkanya bisa di bagi 3 atau habis di bagi 3.
• Pita berwarna putih memiliki angka yang apabila di bagi dengan 3 selalu bersisa 1. Silahkan kalian bagi angka pada warna putih (misalnya 4) 4 : 3 sisanya 1.
  (gunakan cara bagi kurung untuk mengetahui sisanya)
• Pita berwarna biru memiliki angka yang apabila di bagi 3 selalu bersisa 2. Silahkan kalian bagi angka pada warna biru (misalnya 5) 5 : 3 sisanya 2.
  (gunakan cara bagi kurung untuk mengetahui sisanya)

Sekarang kita cek angka 437 jika di bagi oleh 3. 437 : 3 (gunakan cara bagi kurung) sisanya adalah 2. Sehingga 437 ada di kotak berwarna Biru.

Masalah 3: 3 Ekor Kucing

Ibnu memiliki 3 ekor kucing berukuran besar, sedang dan kecil. Ibnu selalu adil dalam memberi makan kucing-kucingnya, yaitu 24 sendok makanan kucing yang dibagi rata untuk semua kucing-kucingnya. Namun setelah di perhatikan, kucing yang berbadan besar selalu merasa kurang sedangkan kucing yang berukuran kecil selalu menyisakan makanannya, dan kucing yang berukuran sedang merasa makanannya cukup.

Dapatkah kalian membantu Ibnu dalam membagi 24 sendok makanan kucing sehingga semua kucing merasa tercukupi?

Penyelesaian 3:

Jika Ibnu membagi rata porsi makanan untuk kucing-kucingnya. Maka setiap kucing memperoleh 8 sendok.

Kucing Besar = 8 sendok

Kucing Sedang = 8 sendok

Kucing Kecil = 8 sendok

Jumlah 24 sendok

Agar semua kucing merasa tercukupi, maka penyelesaiannya kucing besar harus bertambah porsinya dan kucing kecil harus berkurang.

Kucing Besar = 8 sendok + (?) sendok = 8 + 2 sendok = 10 sendok

Kucing Sedang = 8 sendok (tetap) = 8 sendok

Kucing Kecil = 8 sendok - (?) sendok = 8 - 2 sendok = 6 sendok

Jumlahnya 24 sendok

Sehingga porsi yang harus diberikan agar semua kucing merasa tercukupi adalah:

Kucing Besar = 10 sendok

Kucing Sedang = 8 sendok

Kucing Kecil = 6 sendok

Masalah 4: 3 Ekor Kucing versi bilangan berurutan ganjil genap

Cermati masalah 3 di atas lalu kaitkan cara penyelesaian masalahnya untuk mengerjakan masalah berikut:

1. Dapatkah kalian menemukan, tiga bilangan genap berurutan yang jumlahnya adalah 108?
2. Dapatkah kalian menemukan, tiga bilangan ganjil berurutan yang jumlahnya adalah  63?

Penyelesaian 4:

1. Tiga bilangan genap berurutan yang jumlahnya 108.

108 : 3 = 36

36 + 36 + 36 = 108

(36+2) + 36 + (36-2) = 108

38 + 36 + 34 = 108

Jadi tiga bilangan genap berurutan yang jumlahnya 108 adalah 34, 36, 38.

2. Tiga bilangan ganjil berurutan yang jumlahnya 63.

63 : 3 = 21

21 + 21 + 21 = 63

(21+2) + 21 + (21-2) = 63

23 + 21 + 19 = 63

Jadi tiga bilangan ganjil berurutan yang jumlahnya 63 adalah 19, 21, 23.

Masalah 5: Kode Rahasia

Untuk bisa memenangkan lomba teka teki, Riza harus bisa memecahkan kode misteri di setiap babaknya.

• Pada babak pertama Riza harus bisa menemukan 3 angka rahasia yang diperoleh dengan menebak angka berikutnya dari sebuah pola bilangan 1, 4, 7, 10, ..., ..., ...
• Pada babak kedua Riza harus bisa menemukan bilangan genap ke-1202. (Petunjuk bilangan genap ke-1 adalah 2, bilangan genap ke-2 adalah 4, bilangan genap ke-10 adalah 20)

Dapatkah kalian membantu Riza dalam menjawab kode rahasia di atas?

Penyelesaian 5:

1. 3 angka berikutnya dari pola bilangan 1, 4, 7, 10, ..., ..., ...

Karena pola bilangan di atas memiliki keteraturan yaitu selalu di bertambah 3, maka 3 angka berikutnya adalah 13, 16, 19

2. Bilangan genap ke-1202?

Bilangan genap ke-1 adalah 2

Bilangan genap ke-2 adalah 4

Bilangan genap ke-3 adalah 6

Bilangan genap ke-4 adalah 8

Bilangan genap ke-5 adalah 10

Bilangan genap ke-n adalah 2 x n (n adalah bilangan)

Bilangan genap ke-1202 adalah 2 x 1202 = 2404

Untuk menguji pemahaman kita pada materi ini, silahkan klik latihan 2 di bawah ini. Kerjakan dengan serius dan sungguh-sungguh.

LATIHAN 2 (KLIK)

Jika masih ada yang belum kalian pahami silahkan hubungi Ibu di grup whatsapp. 

Stay Happy, Stay healthy 💛 Ibook Kiki

Read More

Matematika VIII : Apa saja yang kita pelajari di kelas VIII?

Hi Assalamualaikum Moorid Moorid 💛

Ibu ucapkan Selamat Datang di jenjang kelas VIII. Pada kesempatan kali ini ibu akan memberikan penjelasan tentang apa saja yang akan kita pelajari di kelas VIII, silahkan kalian simak gambar di bawah ini:

(Di klik gambarnya ya supaya jelas terbaca)

Bagaimana, sudah terbayang kan apa saja yang akan kita pelajari di kelas VIII? Tanamkan dalam hati dan pikiran bahwa matematika itu ga selalu belajar yang susah-susah, kalian pasti bisa dan mampu menguasainya.

Selamat belajar yaa, Jangan lupa  leave some comments atau boleh tanya2 seputar soal-soal matematika  (insyaAllah) I'll answer it right away.

Stay Happy, Stay healthy 💛 Ibook Kiki

Read More

BILANGAN BULAT | 3. Perkalian dan Pembagian Bilangan Bulat

Hi Assalamualaikum Moorid Moorid 💛

Sebelum kita mulai belajar, mari kita sama-sama berdoa agar pembelajaran hari ini lancar dan lanjutkan dengan mengisi kehadiran melalui link bawah ini (klik sesuai kelas):

KELAS 7F                    KELAS 7G                KELAS 7H

Pada kegiatan kali ini kita akan mempelajari tentang "PERKALIAN & PEMBAGIAN BILANGAN BULAT".Untuk memahami bagaimana cara menghitung perkalian dan pembagian bilangan bulat, yuk kita review kembali pembelajaran kita mengenai "Penjumlahan dan Pengurangan Bilangan Bulat". Setelah kalian menyimak kembali materi mengenai penjumlahan bilangan bulat, apakah kalian menemukan hubungan antara konsep perkalian dan penjumlahan bilangan bulat?

Contoh sederhana: Berapakah hasil kali 5 x 6 ?

Penyelesaian:

5 x 6 = 6 + 6 + 6 + 6 + 6 = 30

Jadi hubungan antara Konsep perkalian dan penjumlahan adalah, perkalian merupakan penjumlahan berulang.

Pada operasi perkalian, juga berlaku sifat komutatif, asosiatif dan distributif.

1. Sifat komutatif : a x b = b x a

2. Sifat Asosiatif : a x (b x c) = (a x b) x c

3. Sifat Distributif : a x (b + c) = (a x b) + c

Masih ingatkah kalian mengenai aturan perkalian pada bilangan bulat yang sudah kalian pelajari di Sekolah Dasar:

Aturan Perkalian Bilangan Bulat

Suatu bilangan negatif jika dikalikan dengan bilangan positif makan hasilnya NEGATIF. Namun jika bilangan negatif dikalikan dengan bilangan negtaif maka hasilnya POSITIF. Oke kita kembali ke penyelesaian permasalahan di atas.

Agar semakin jelas mari kita simak permasalahan perkalian dalam kehidupan nyata di bawah ini:

Masalah 1 : Lomba Matematika

Andri dan Bono adalah peserta yang telah selesai mengikuti babak final dalam perlombaan cepat tepat matematika. Sebelum diumumkan siapa yang berhasil memenangkan perlombaan, Panitia harus menghitung skor yang mereka peroleh. Aturan penghitungan skor seperti di bawah ini:

Jawaban benar memperoleh skor 5

Jawaban salah memperoleh skor -3

Dan untuk soal yang tidak di jawab, skor nya 0

Dari 20 soal yang diujikan, Andri menjawab 15 soal dan 12 soal berhasil di jawab dengan benar, sedangkan Bono menjawab 18 soal dan hanya 5 soal yang salah.

Menurut kalian, siapakah yang berhasil memenangkan lomba?

Penyelesaian 1:

Diketahui:

Andri menjawab 15 soal dari total 20 soal dan 12 jawaban benar

Bono menjawab 18 soal dari total 20 soal dan 5 soal salah

Ditanya:

Siapakah yang menang?

Jawab:

Andri menjawab 15 soal dari total 20 soal dan 12 jawaban benar, berarti:

5 soal tidak terjawab x 0 = 0

12 soal benar x 5 = 60

3 soal salah x (-3) = -9

Total Skor Andri = 0 + 60 + (-9) = 51

Bono menjawab 18 soal dari total 20 soal dan 4 soal salah, berarti:

2 soal tidak terjawab x 0 = 0

13 soal benar x 5 = 65

5 soal salah x (-3) = -15

Total Skor  Bono = 0 + 65 + (-15) = 50

Jadi yang berhasil memenangkan lomba adalah Andri.

Bagaimana? Cukup mudahkan? Semoga kalian paham ya. Jika belum, kalian boleh tanya lewat WA Grup atau tulis komen di bawah ya. Lanjut ke masalah selanjutnya tentang pembagian.

Apakah pembagian bilangan bulat memiliki aturan yang sama dengan perkalian bilangan bulat?  Untuk mengetahui jawabannya, mari kita simak simulasi di bawah ini.

Berdasarkan simulasi di atas, Apakah aturan pembagian sama dengan aturan perkalian? Tentu jawabannya sama. Mudah kan mengingatnya.

Apakah sifat komutatif, asosiatif dan distributif berlaku juga di pembagian? Mari kita lakukan simulasi sederhana untuk menjawab pertanyaan di atas.

1. 8 : 2 apakah hasilnya sama dengan 2 : 8?, jika jawabannya sama maka sifat komutatif berlaku pada pembagian.
2. 8 : ( 4 : 2) apakah hasilnya sama dengan (8 : 4) : 2?, jika jawabannya sama maka sifat asosiatif berlaku pada pembagian.
3. 8 : ( 2 + 2) apakah sama hasilnya dengan (8 : 2) + (8 : 2)?, jika jawabannya sama maka sifat distributif berlaku pada pembagian.

Jadi bagaimana menurut kalian? apakah sifat komutatif, asosiatif dan distributif berlaku pada pembagian?

Untuk lebih memahi pembagian pada bilangan bulat, mari kita lanjutkan dengan menyimak masalah di bawah ini.

Masalah 2 : Study Tour

Seluruh murid kelas VII A - VII H dan wali kelasnya akan mengikuti study tour ke Museum PP IPTEK dengan menggunakan Bus. Jika jumlah murid pada setiap kelas adalah 30 orang dan 1 bus hanya bisa diisi oleh 62 orang. Maka berapa banyak bus yang harus di sediakan Sekolah untuk menampung seluruh murid dan wali kelasnya?

Penyelesaian 2:

Diketahui:

Jumlah kelas (VII A sampai VII H) = 8 kelas

Jumlah murid per kelas dan wali kelasnya = 30 orang + 1 orang = 31 orang

Kapasitas/ daya tampung 1 bus = 62 orang

Ditanya:

Jumlah bus yang dibutuhkan?

Jawaban:

Jumlah total yang mengikuti study tour = 31 orang x 8 kelas = 248 orang

Kapasitas bus = 62 orang

Jumlah bus yang dibutuhkan = 248 : 62 = 4 bus

Bagaimana? Cukup mudahkan? Semoga kalian paham ya. Jika belum, kalian boleh tanya lewat WA Grup atau tulis komentar di bawah ya.

Kalian telah memelajari empat macam operasi pada bilangan bulat, yaitu penjumlahan (+), pengurangan (−), perkalian (×), dan pembagian (÷). Misal ada suatu soal matematika sebagai berikut.

Tentukan hasil dari 6 + 2 × 4 = ...

Kemungkinan jawaban pertama 6 + 2 × 4 = 8 × 4 = 32
Kemungkinan jawaban kedua 6 + 2 × 4 = 6 + 8 = 14

Menurut kalian, jawaban manakah yang benar? Jelaskan alasanmu. Jika tidak dibuat aturan dalam urutan operasi matematika, maka dalam perhitungan matematika akan menghasilkan beberapa kemungkinan jawaban yang berbeda seperti di atas. Oleh karena itu, para matematikawan sepakat untuk membuat aturan tentang urutan operasi.

"KURUNG, PANGKAT, KALI BAGI (ditentukan dari yang paling kiri), TAMBAH KURANG (ditentukan dari yang paling kiri)"

Contoh soal:

Hasil dari (-12) : 3 + (-8) x (-5) adalah...

Penyelesaian:

Berdasarkan urutan

Urutan 1: Pembagian karena posisinya paling kiri dari perkalian.

(-12) : 3 = -4

Urutan 2: Perkalian

(-8) x (-5) = 40

Urutan 3: Penjumlahan

(-4) + 40 = 36

Jadi hasil dari (-12) : 3 + (-8) x (-5) = 36

Bagaimana? Mudah bukan. Silahkan ajukan pertanyaan di kolom komentar atau di WAG (bagi murid SMP 14) jika ada yang masih belum kalian pahami atau pertanyaan-pertanyaan lainnya seputar Perkalian dan Pembagian bilangan bulat.

Alhamdulillah materi mengenai Perkalian dan Pembagian bilangan bulat sudah selesai. Selanjutnya kita akan menguji pemahaman kita mengenai materi yang baru saja kita pelajari dengan cara mengerjakan Kuis 3 via Googleform di bawah ini. Selamat mengerjakan.

KUIS 3 CEK

Stay Happy, Stay healthy 💛 Ibook Kiki

Read More